| آموزش انتگرال به همراه فرمولهای انتگرال |  |
 |
 |
| شنبه ۲۱ آذر ۱۳۸۸ ساعت ۰۸:۴۶ |
|
آموزش انتگرال
انتگرالها يک بحث اساسي رياضيات عالي را تشکيل داده که ميتوان کاربرد آنرا درتمام علوم طبيعي، انساني وغيره مورد مطالعه قرارداد. اولين بار لايب نيتس نماد استانداردي براي انتگرال معرفي کرد. از لحاظ تاريخي dx يک کميت بي نهايت کوچک را نشان ميدهد. هر چند در تئوريهاي جديد، انتگرال گيري بر پايه متفاوتي پايه گذاري شده است. تابع اوليه هر گاه معادله مشتق تابعي معلوم باشد وبخواهيم معادله اصلي تابع را تعيين کنيم اين عمل را تابع اوليه مي ناميم. تعريف: تابع اوليه y = f(x)را تابعي مانند Y = F(x) + c مي ناميم،هرگاه داشته باشيم: cعدد ثابت (y = F(x) + c)' = y = f(x) انتگرال نامعين تعريف:هرگاه معادله ديفرانسيلي تابعي معلوم باشد وبخواهيم معادله اصلي تابع را معلوم کنيم اين عمل راانتگرال نا معيين ناميده و آن را با نماد بنا به تعريف نماد انتگرال معين بنا به تعريف نماد aوb را به ترتيب کرانهاي بالا و پايين انتگرال ميناميم. تابع انتگرالپذير اگر تابعي داراي انتگرال باشد به آن انتگرالپذير گويند. تعبير هندسي انتگرال از نظر هندسي انتگرال برابر است با مساحت سطح محصور زير نمودار.
انتگرال يک تابع مثبت پيوسته در بازه (0,10) در واقع پيدا کردن مساحت محصور بين خطوط x=0 , x=10 و خم منحني fx است. aو b نقاط ابتدا و انتهاي بازه هستند و f تابعي انتگرالپذير است و dx نمادي براي متغير انتگرال گيري است. انتگرال يک تابع مساحت زير نمودار آن تابع است. انتگرال گيري انتگرال گيري به معني محاسبه سطح زير نمودار با استفاده از روشها وقوانين انتگرال گيري است. 1.f تابعي در بازه (a,b) در نظر ميگيريم. 2.پاد مشتق f را پيدا ميکنيم که تابعي است مانند f که و داريم: 3.قضيه اساسي حساب ديفرانسيل و انتگرال را در نظر ميگيريم:
بنابراين مقدار انتگرال ما برابر خواهد بود. به اين نکته توجه کنيد که انتگرال واقعاً پاد مشتق نيست (يک عدد است) اما قضيه اساسي به ما اجازه ميدهد تا از پاد مشتق براي محاسبه مقدار انتگرال استفاده کنيم. معمولاً پيدا کردن پاد مشتق تابع f کار سادهاي نيست و نياز به استفاده از تکنيکهاي انتگرالگيري دارد اين تکنيکها عبارتاند از :
روش هايي ديگر نيز وجود دارد که براي محاسبه انتگرالهاي معين به کار ميرود همچنين ميتوان بعضي از انتگرال ها با ترفند هايي حل کرد براي مثال ميتوانيد به انتگرال گاوسي مراجعه کنيد. محاسبه سطح زير نمودار بهوسيله مستطيل هايي زير نمودار. هر چه قدرعرض مستطيل ها کوچک ميشوندمقدار دقيق تري از مقدار انتگرال بدست ميآيد.
جدول كامل فرمول هاي انتگرال
Rules for integration of general functions Rational functions Irrational functions Logarithms Exponential functions Trigonometric functions |
نظرات شما عزیزان:


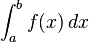 aو b نقاط ابتدا و انتهاي بازه هستند و f تابعي انتگرالپذير است و dx نمادي براي متغير انتگرال گيري است.
aو b نقاط ابتدا و انتهاي بازه هستند و f تابعي انتگرالپذير است و dx نمادي براي متغير انتگرال گيري است.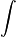 نمايش مي دهند.
نمايش مي دهند.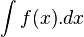 را انتگرال نامعين ناميده وحاصل آن را تابعي مانند
را انتگرال نامعين ناميده وحاصل آن را تابعي مانند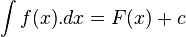 با شرط:
با شرط: 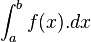 را انتگرال معين ناميده و حاصل آن را عددي به صورت زير تعريف ميکنيم: a
را انتگرال معين ناميده و حاصل آن را عددي به صورت زير تعريف ميکنيم: a

![int [f(x) + g(x)],dx = int f(x),dx + int g(x),dx](http://upload.wikimedia.org/math/e/7/d/e7d070d203baf49797b4e4a3fc3685f3.png)
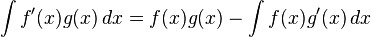

![int {f'(x) f(x)},dx= {1 over 2} [ f(x) ]^2 + C](http://upload.wikimedia.org/math/0/c/6/0c64f04cc80db157abf9bbb321648b42.png)
![int [f(x)]^n f'(x),dx = {[f(x)]^{n+1} over n+1} + C qquadmbox{(for } nneq -1mbox{)},!](http://upload.wikimedia.org/math/e/8/9/e892e0442b228299602a1f87b51ec430.png)

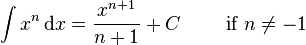
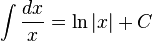
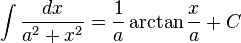

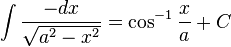

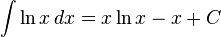

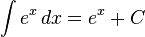
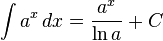



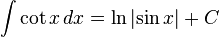








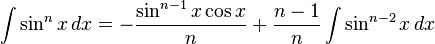












![int operatorname{arccsch},x , dx = x operatorname{arccsch} x+ log{left[xleft(sqrt{1+frac{1}{x^2}} + 1right)right]} + C](http://upload.wikimedia.org/math/4/c/4/4c4828d0c47957eb215c2249b1c64fa7.png)

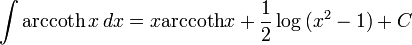

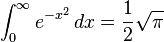



 )
)  is an odd integer and
is an odd integer and 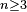 )
) 

![int_{-infty}^infty e^{-(ax^2+bx+c)},dx=sqrt{frac{pi}{a}}expleft[frac{b^2-4ac}{4a}right]](http://upload.wikimedia.org/math/3/1/8/31880cca3462a0bd5cc1e00bbc790da9.png)
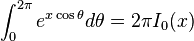

 (
( 0\," />,
0\," />, 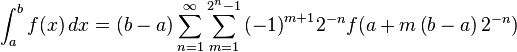

 آمار
وب سایت:
آمار
وب سایت:

